Zero-centered Re-parameterization of LayerNorm

First Published on 5/25/2025
Updated on 9/15/2025
Update (9/15/2025): Thanks to Qwen for adopting and using one of our inventions in this article in their model release last week.
By Yi Liu, Tom Costello and Sean Costello
Tldr;
Norms have weights, but these should be stored as values near zero, as that gives better accuracy. Zero-centering also allows us to weight-decay these values properly. Some models (Llama, phi, and Olmo) seem to weight decay their norm weights to zero, which seems wrong. Others (Qwen, Mistral, Fairy-R1) show slowly growing norm weights, suggesting no weight decay. Gemma, in particular, seems not to have any weight decay, as their weights balloon to huge values (~300) in later layers. Gemma even has some negative values for weight norms, which shows that something very weird happened during training. We have some theories on why this happens.
Zero center your values. Weight decay to the natural answer. Check your weights are not doing crazy things.
Introduction and Theory
In scaling large language models, we are always interested in saving memory, sometimes by reducing the precision of the learned parameters. LayerNorm plays a key role in rescaling the distributions of activations. At the same time, cutting too much precision can result in poor model performance. This tradeoff between memory use and precision presents an important Pareto curve to improve. We observe an opportunity to improve how we quantize the post-normalization scaling parameter, gamma, compared to standard practice. The definition of LayerNorm is provided below.

The gamma parameter is multiplied by the normalized activations in LayerNorm. Usually, it is not subject to L2-regularization. Initialization of gamma to 1.0 makes sense because it corresponds to not doing any scaling. In fact, we would typically expect learned gamma parameters to be centered near 1.0.
This precision is highly relevant to the quality of the forward pass during training and inference. During training, specifically, the precision is further relevant to how well the optimizer can accumulate very small numbers onto the weights.
Since gammas should be near 1.0, we refer to gamma values close to 1.0 as having low entropy and being low-bit. These low-bit gamma values deserve to occupy the most precise parts of the parameter space. Currently, the common practice is to parameterize these gammas as a raw floating-point parameter.
Floating point representations allocated their finest precision for values near 0. To maximize low-bit floating point accuracy, we want the learned parameters to sit where the floating-point bins are smallest, around zero. To make the most efficient use of our memory, we should reparameterize the learning so that the low-bit gammas align with where the floating point parameters have the smallest bin sizes. With an offset-by-1 reparameterization, we could achieve this with gamma = omega + 1, with omega serving as our raw zero-centered parameter. We show a plot of some FP8 E5M2 numbers and their local bin sizes below, to visualize that the bins are smaller near zero and larger near 1.
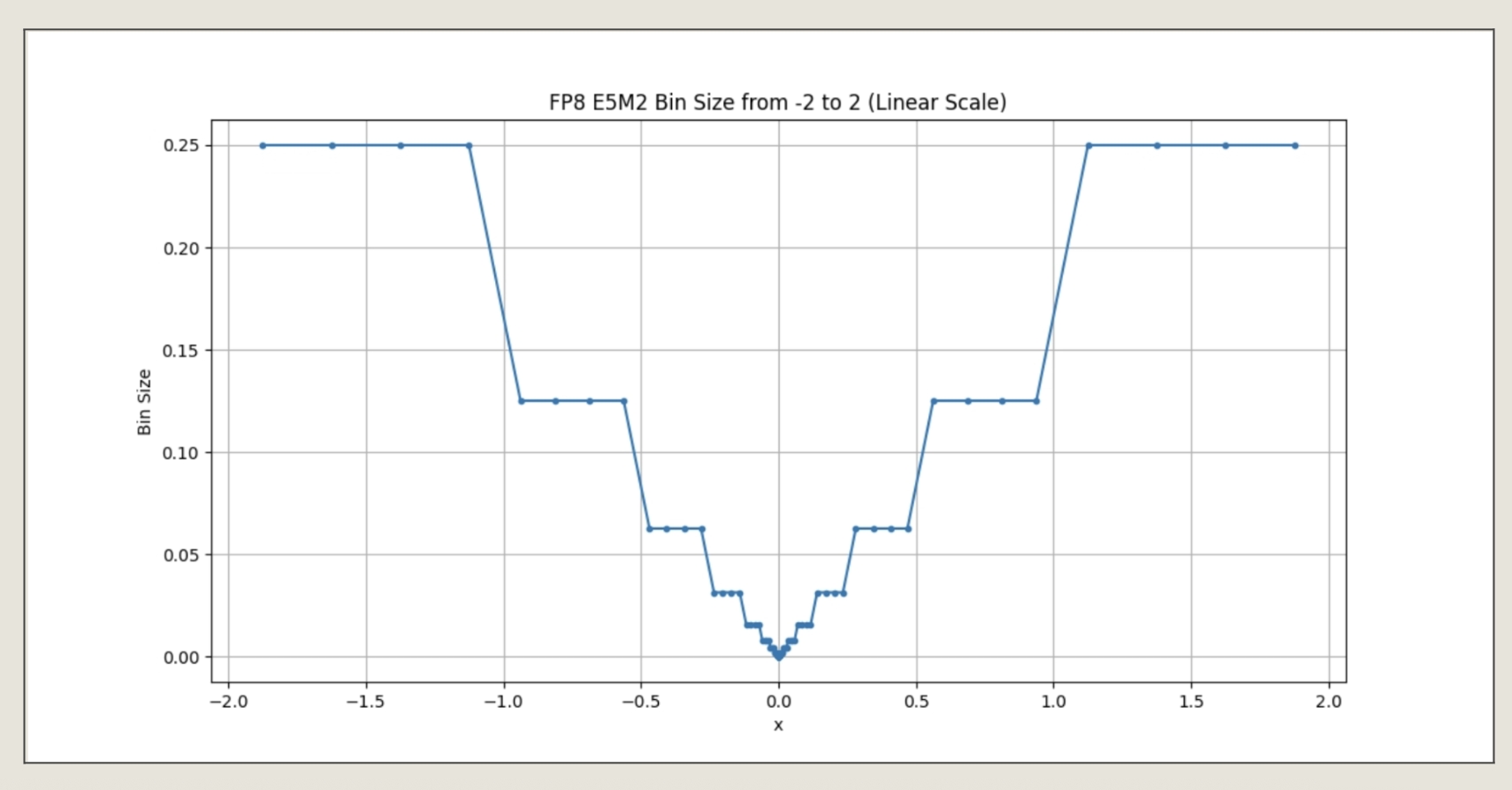
We provided an implementation below in torch to illustrate. We introduced omega as a floating point learnable zero-centered parameter, and computed gamma = omega + 1. Initialized omega_0 to be 0 to preserve standard initialization, while centering the floating point optimization around zero.
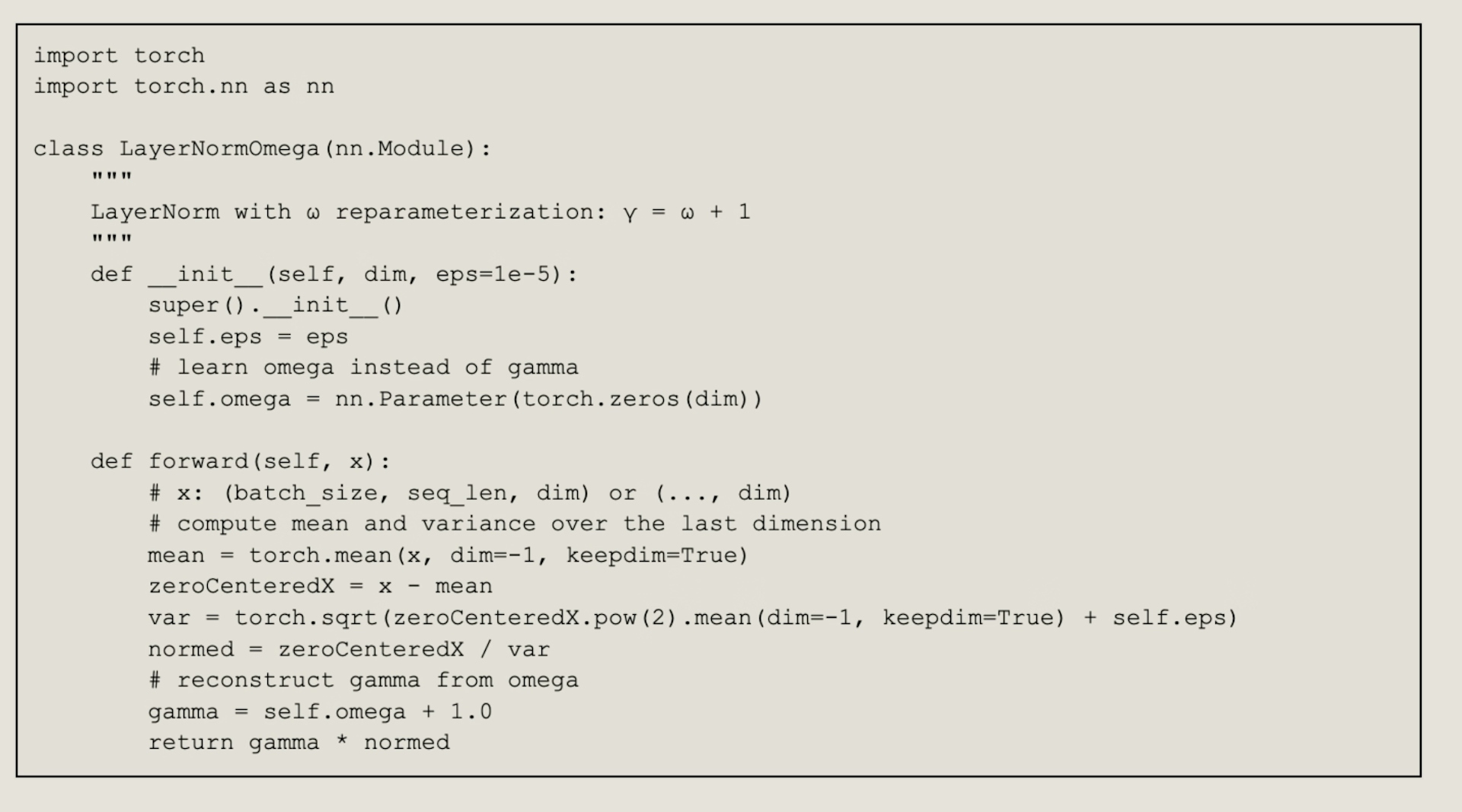
Because omega sits at 0 for the identity scaling, applying weight directly would encourage a pass-through behavior. This is an open question, around weight decay for gamma, which may further stabilize training.
We provided a table of benefits and drawbacks of the zero-centered omega reparameterization. This example illustrates a broader principle that we should zero-center or floating-point parameterizations.
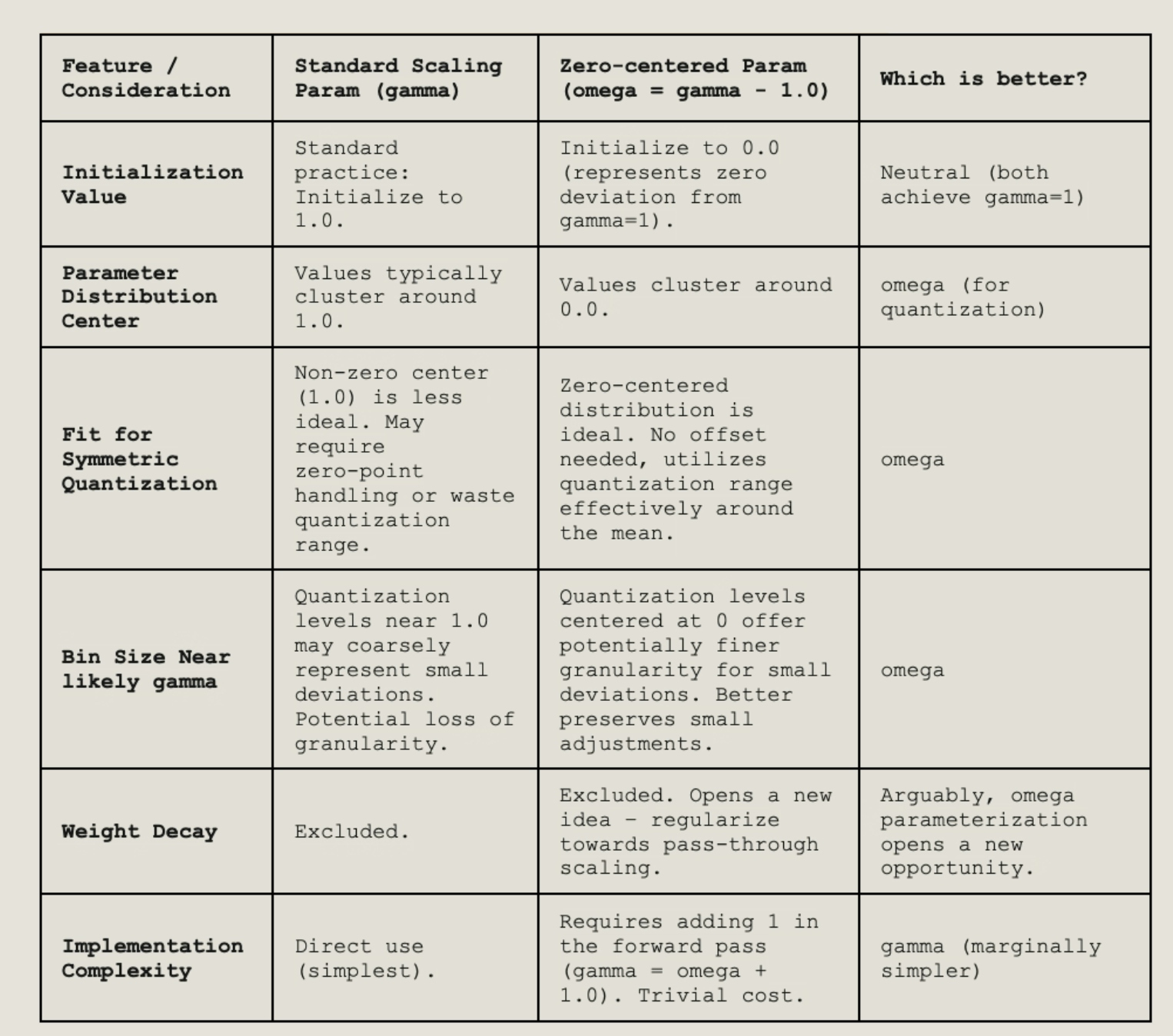
Table 1. Comparison of Zero-centered Omega and Standard Scaling
Floating-point representations have their finest precision near zero, but the gamma coefficients in LayerNorm should cluster near one. We’ve discussed how an offset reparameterization can zero-center the learned parameter, and resolve this numerical mismatch. Importantly, we present this observation as a general principle: whenever a learned parameter naturally centers away from zero, recentering it can better exploit floating-point precision. This extends beyond normalization layers and applies broadly to floating-point learning.
How should we weight decay normalization layers?
Weight decay with L2 is a broad regularization technique that applies an L2 loss to learned parameters. It offers typical regularization benefits like generalization and optimization stability.
The general community generally prefers to not decay the learned parameters in normalization layers. For example, see this issue in miniGPT, another issue in transformers, and a pytorch forum discussion. This is not yet universal in practice, as for example, AllenAI’s Olmo2 training yaml suggests that their norm layer parameters are subject to weight decay. The role of gamma in the norm layers is multiplicative, and so the identity of that operation is 1.0, rather than 0. If we were to regularize, gamma 1.0 is actually the more natural, “smaller”, regularization target. With our centered omega reparameterization, gamma towards 1.0 conveniently becomes decaying omega towards zero. In the next section we will take a look at the distribution of these learned gamma values in open source pre-trained models.
Distributions of RMSNorm Gamma in Pre-trained Models
We would be interested in understanding whether real trained models do empirically center around 1. To address this, we loaded up a few LLMs from Huggingface and plotted their gamma values. We collected all the norm layers in the stacked transformers, and checked the means and variances of their gamma values. Each module is plotted with a single point. Different markers would indicate the architectural position inside a transformer, and we used a color map to communicate the depth. Generally, there is a clear pattern to the norm values as you go into the deeper layers, with increasing variances as you go deeper layers. We note that the pattern is different across architectures. We show in Figure 1 and summarize in Table 2.

Table 2. Largest mean gammas seen. Individual values can be even more extreme.
For Gemma 3, the gamma means can go as high as 300 and can also go negative for some layers. We would not expect it to be an optimal situation for training. In contrast, the gamma values for Olmo-2, Llama3 and Phi4 lie between 0 and 1 and appear to be much better controlled. We didn’t know the precise training recipes, but Olmo-2 appears to regularize their normalization weights. We wonder if the Gemma 3 model could especially benefit from regularization, especially of a reparameterized omega towards 0 (or alternatively written, regularization of gamma towards 1). Unfortunately, we do not have experiments scaled to reproduce these training phenomena in their norm gammas.
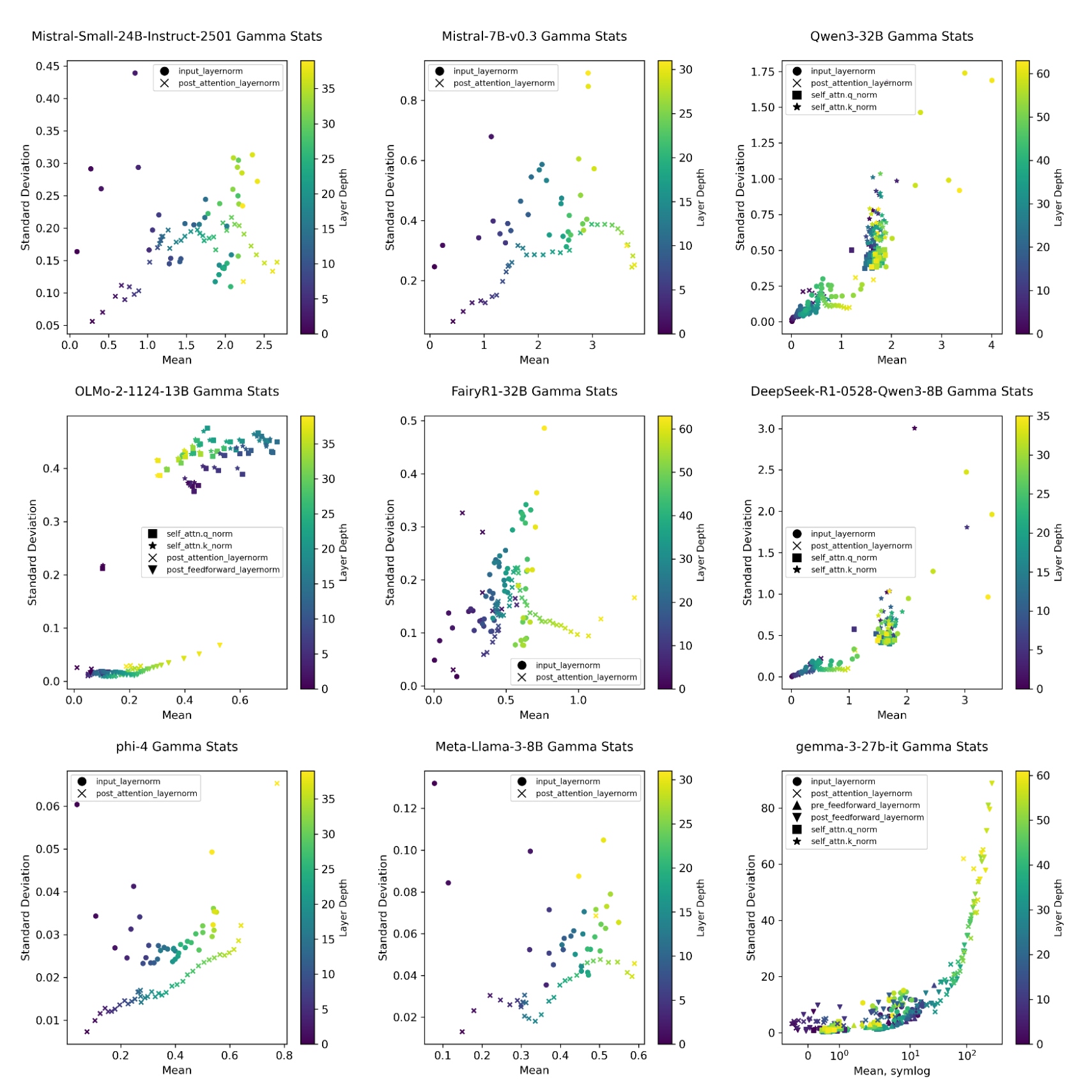
Figure 1: Gamma means and variances tend to grow in the deeper layers. Some models like Gemma 3 have negative and also very large gamma values (note the symlog x-axis). Olmo, Llama, and phi are particularly restricted to between 0 and 1.
We found these extreme values in Gemma 3 intriguing, and we provide some ideas on how this can arise.
- Multiplicative parameters, under SGD, creating quadratic step sizes on the effective product coefficient. The quadratic steps sizes can cause poor training dynamics. There is lack of weight decay on gamma, while there is weight decay on linear layer weights. This asymmetry can cause gamma to absorb magnitudes from the weights.
- Work from various sources have observed high variance and norm in late layers, and attribute training instability to them.
https://arxiv.org/abs/2502.05795 (Curse of Depth)
https://arxiv.org/abs/2503.17500 (Weight Rescaling)
https://arxiv.org/abs/2502.02732 (Peri-LN) - For deeper layers, the linear layers deeper in the network can try to stay relevant during training by increasing the effective norms of the weights in later layers. However, most models are trained with weight decay, whereas the RMSNorm gammas are not subject to decay, and so the increases in the aggregate norm could be absorbed by the gammas over time.
https://arxiv.org/pdf/2505.13898 (Csordás, Manning, Potts) - AdamW Optimizers, in the formulation, generally assume independence of gradients in the time domain. When this correlation breaks, it can lead to training instability. RMSNorm gamma gradients are subject to more axes of averaging, compared to individual entries of linear layer weights, which would amplify the unmodeled correlations.
https://arxiv.org/pdf/2304.09871 (Adam Instability, Meta)
In this blog, we focus a bit more on the dynamics of the product coefficient as there is something simultaneously dangerous and also subtle to identify. While analyzing the interaction between RMSNorm (or LayerNorm) and subsequent linear layers, we saw something subtle about how these components behave quadratically together during training.
Products of learned parameters take quadratic steps in each factor
Found in most modern transformers, a normalized input x gets multiplied by gamma from the normalization layer, then by weight matrix W from the linear layer. When we examined how these gamma values evolve during training, we found a quadratic relationship that raises questions about extremely large gamma values. In the previous section (figure 1), we saw very large gamma means observed in the deeper layers of models like Gemma 3 with values in the hundreds.
Let’s mentally picture the intermediate coefficient, V = gamma * W . This intermediate coefficient depends entirely on the underlying parameters gamma and W, and its per-step update, when expanded, turns out to be quadratic in both gamma and W. This mathematical observation reminds us that the optimization is substantially influenced by the parametrization. We wonder whether the Qwen and Gemma teams simply tolerated these large effective steps. The intermediate product, overparameterized by two SGD learned parameters, receives effectively quadratically-scaled update steps. This could explain some of the empirical troubles with making best use of deeper transformer layers. We provide a brief write-up (see derivation notes 1) of the detailed mathematical framing. The analysis is a comment on the gradient magnitudes, and so the use of AdamW would not fully address the gradient explosion issue. The mathematical framing is provided in Math section 1.

Math Section 1. The product coefficient when a linear layer follows an RMSNorm
To work out the math for the effective update to the product, one would apply the update rules, calculate the new product V, express that as a polynomial in the learning rate eta, and check the coefficient of the first order term. On first inspection of the effective product learning rate, one might see two places where the effective updates get large, there appears to be a term quadratic in gamma, and also one that is inverse quadratic. We explore this quadratic update in Math Section 2.

Math Section 2. The product V has step updates quadratic in gamma
Experiments and Discussion
We tested some controlled experiments to test whether our observations above on zero-centered learning would lead to practical improvements. All runs were trained on 32 A100s over the course of 1 epoch, on a mixture of Wikipedia and Arxiv data from the RedPajama 1T dataset, initialized from scratch on a 500M architecture based on Llama3.
We also tried tweaking the learning rate specific to gamma and omega to see if there are any interactions. We tried increasing just the learning rates on just the RMSNorm modules by a factor of 100, and we did not see strong effects. The general learning rate was 1e-4 throughout. This suggests that we are not in a regime sensitive to the step sizes of those particular parameters. See Table 3 for details..
We plotted the distributions and variances for post-attention-layernorm gammas in final converged models, for each of the 21 transformer blocks in our Llama3 model. We saw that there is a small systematic reduction of variance when weight decay is applied to the gammas, evenly spread across all the layers. When the learning rates for Layernorm are increased by 10x and 100x, weight decay results in a further reduction of variance, compared to the gamma parameterized counterparts with the same learning rate change. As we increase the learning rate on the LayerNorm modules, the reduction becomes less equally spread across all the layers.
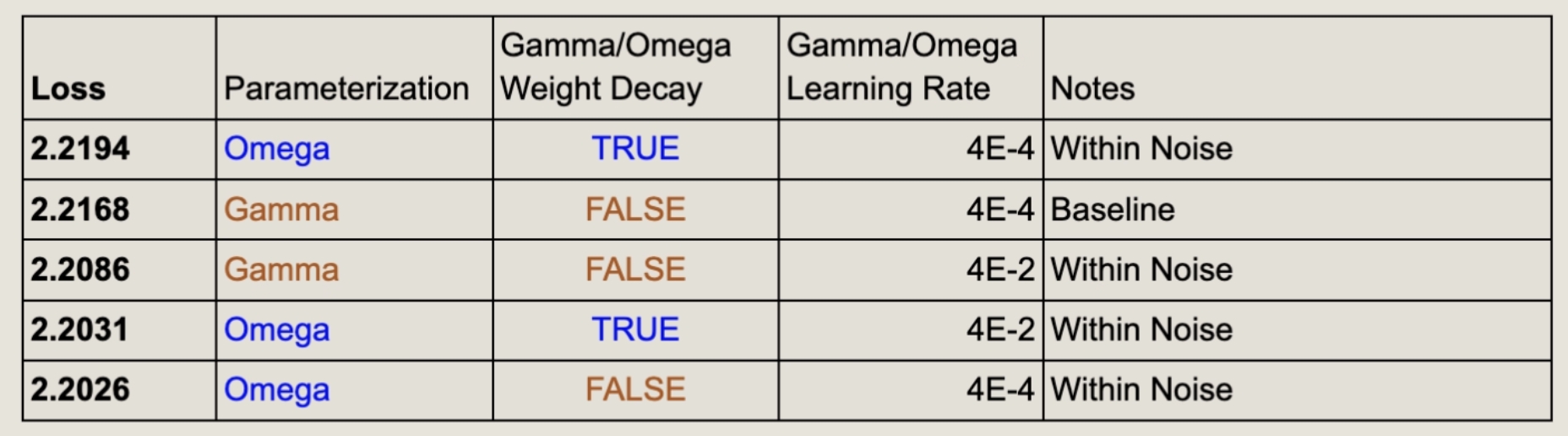
Table 3: Empirical Results. Largely within noise.
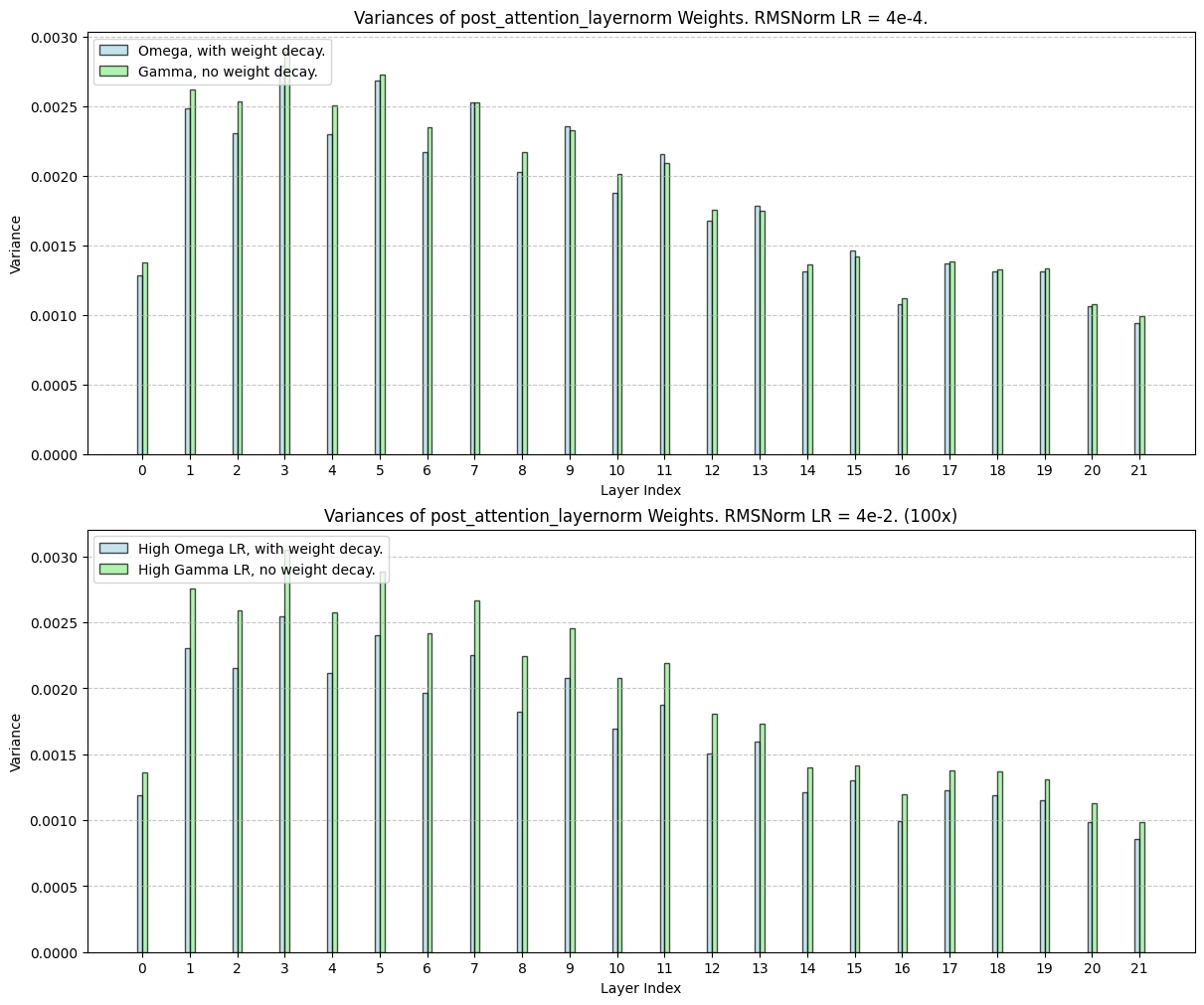
Figure 2: Weight decay on Omega systematically decreases the variances in the learned parameters. This effect grows larger when we ramp the learning rate for just the LayerNorm to 100x.
Conclusion
In our investigation of zero-centered reparameterization for LayerNorm, we explored the potential advantages of shifting our perspective on scaling parameters. Reparameterizing gamma as omega + 1 aims to align learned parameters with the fine precision of floating-point representations, potentially enhancing quantization and training stability.
While the empirical experiments fell within the noise margin, further examination in high learning rate scenarios revealed the potential of weight decay on the omega parameterization. This method systematically reduces the variance in learned parameters, especially when LayerNorm learning rates are significantly increased.
We checked the gamma distributions across models, and particularly Gemma 3, there could be benefit from regularizing the reparameterized omegas towards zero (or gamma towards 1). In our analysis of the effects of parameterization on gradient dynamics, we highlighted a subtle quadratic relationship that arises when multiplicative coefficients are decomposed into product coefficients.
In summary, this exploration highlights a fundamental principle: that we want to align parameter representations with the numerical characteristics of floating-point formats. When learned parameters tend to cluster away from zero, recentering them can better leverage the available precision. This strategy extends beyond normalization layers and offers a valuable approach for optimizing floating-point learning in diverse applications.