Beneath the Surface - the Curse of Depth in AI Training Models

By Lucas Han, Tom Costello and Sean Costello
Recently, the AI community has come to the revelation that the latter half of training layers have next to zero effect on the efficiency of models. You can almost hear it - execs rubbing their hands together with glee, realising that they can cut their costs if they simply stop training later layers. And yet, if performance isn’t correlative to depth, why are so many tech firms wasting their resources on training layers?
LLM training undermines the age-old quote, “Half the money I spent on advertising is wasted; the trouble is, I don’t know which half.” Now we know: it's the latter. This breakthrough questions the very purpose of later layers. Is it simply so you can attach the title “deep” in front of “learning”? If anything, this aggregation of layers can asphyxiate productivity, even leading to vanishing gradients. Csordás et al., 2025 also recently wrote about this phenomenon.
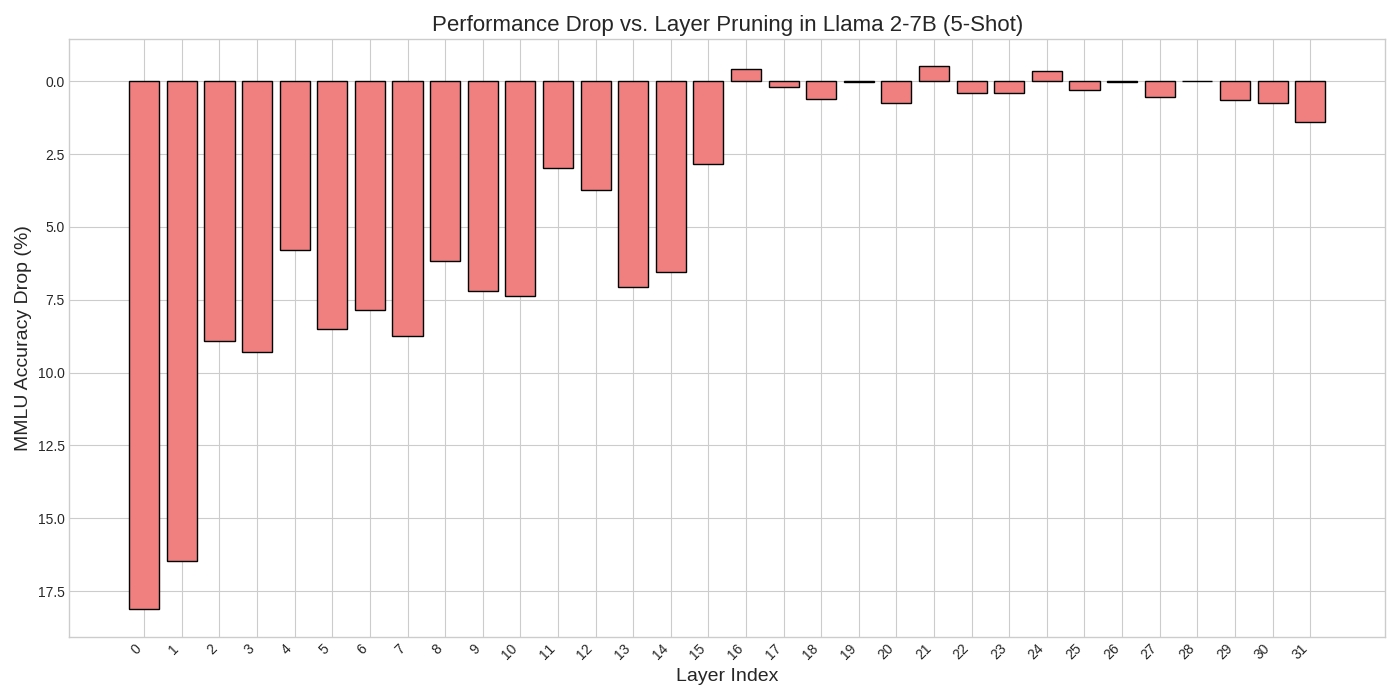
Figure 1 - The bar represents how much removing the layer impacts the performance of Llama2 7B using the MMLU benchmark as the y axis. After layer 16 the cost of removing the layer drops to 1.5 or below.
The paper The Curse of Depth in Large Language Models (Sun et al., 2025) sought a way to fix the Curse of Depth through layer norm scaling. The Ceramic team decided to try our hand at investigating this issue and applying Sun’s solutions to see if they can actually work. The premise - that paying less attention to later layers will make them contribute more - is certainly interesting, and challenges conventional approaches to the issue. Neglecting these layers seems counterintuitive to improving efficiency; would paying your employees less increase productivity? Therefore, we trained 5 Llama3-2B in different systems of approach, driven by the intention to control variances in later layers. The methods we used with the aim of enhancing this process are outlined below. The first two we reproduced previous results: 1) Baseline with no scaling 2) LayerNorm output scaling (CoD scaling Sun et al., 2025), and we introduce three new methods: 3) Scaling of input RMSNorm’s initial weights (gamma scaling) 4) Scaling of input projection weights in attention (q,k,v) and MLP (w1,w2) blocks (input scaling), and finally 5) Scaling of output projection weights in attention (c_proj) and MLP (w3) blocks (output scaling).
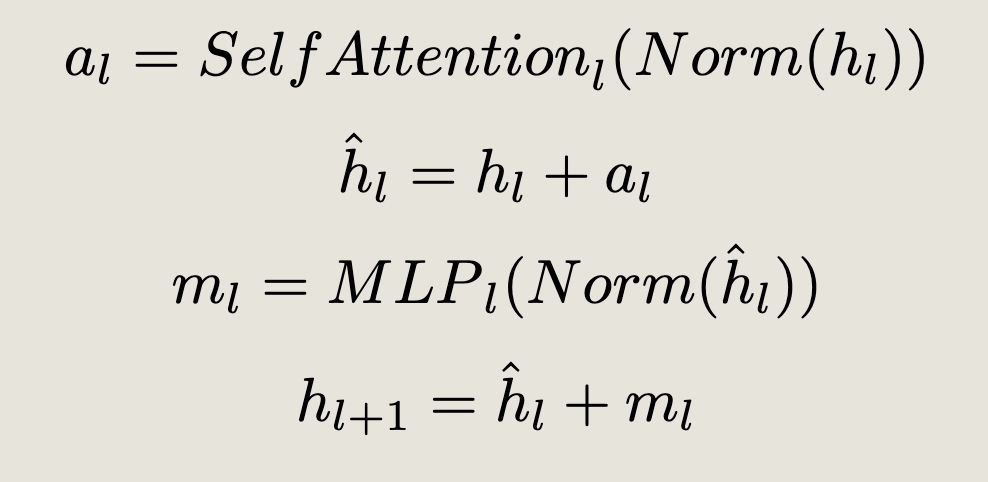
Baseline: Standard Pre-LN Transformer layer
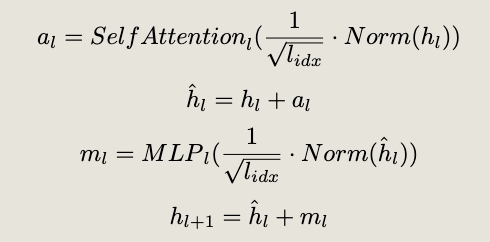
CoD Transformer Layer
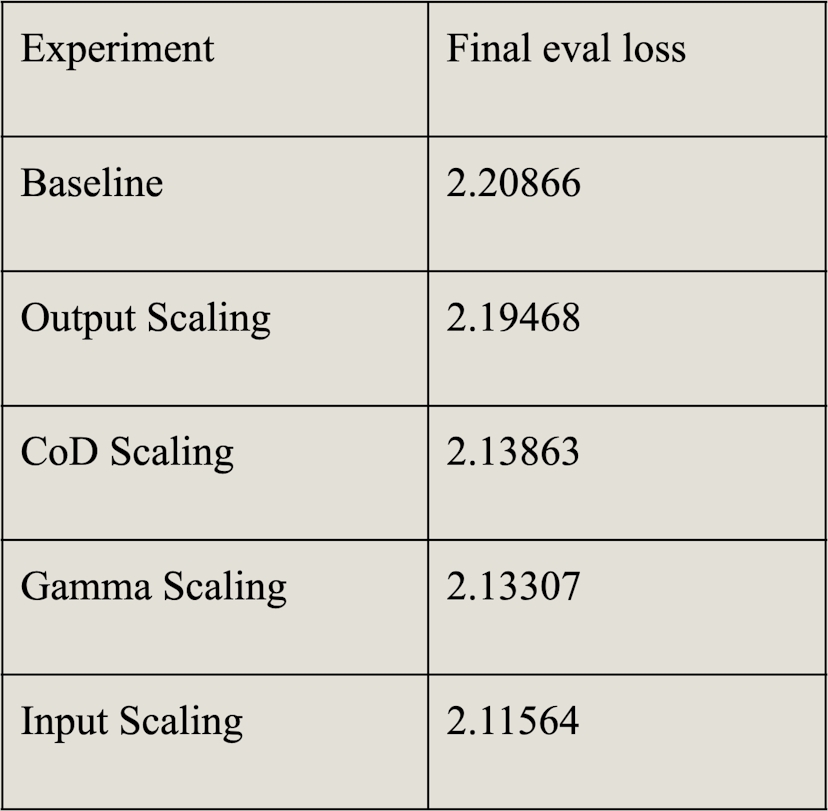
By training models using baseline and CoD, we found that LayerNorm did indeed improve the overall loss, hence Sun’s model appears to hold true. In our study of three alternatives, gamma, input and output, interestingly, input scaling was the clear winner. Among the three strategies it achieves the lowest eval loss. We then made the usual mistake of not being happy with a win. The results from our techniques suggest that instabilities in deeper layers are, in fact, solvable. This begs the question, “why scaling the input weights of attention and MLP outperformed the proposed CoD scaling method?”
Examining attention in greater detail, we identified that the attention scores for baseline and output scaling exhibit uncontrollable growth in pre-softmax attention scores in the later layers.
Responsively, this then pushes the softmax function into a regime where it produces a one-hot distribution. CoD scaling reduces the magnitude of inputs to the attention block, which shrinks the query and key vectors, thereby taming the final attention scores.
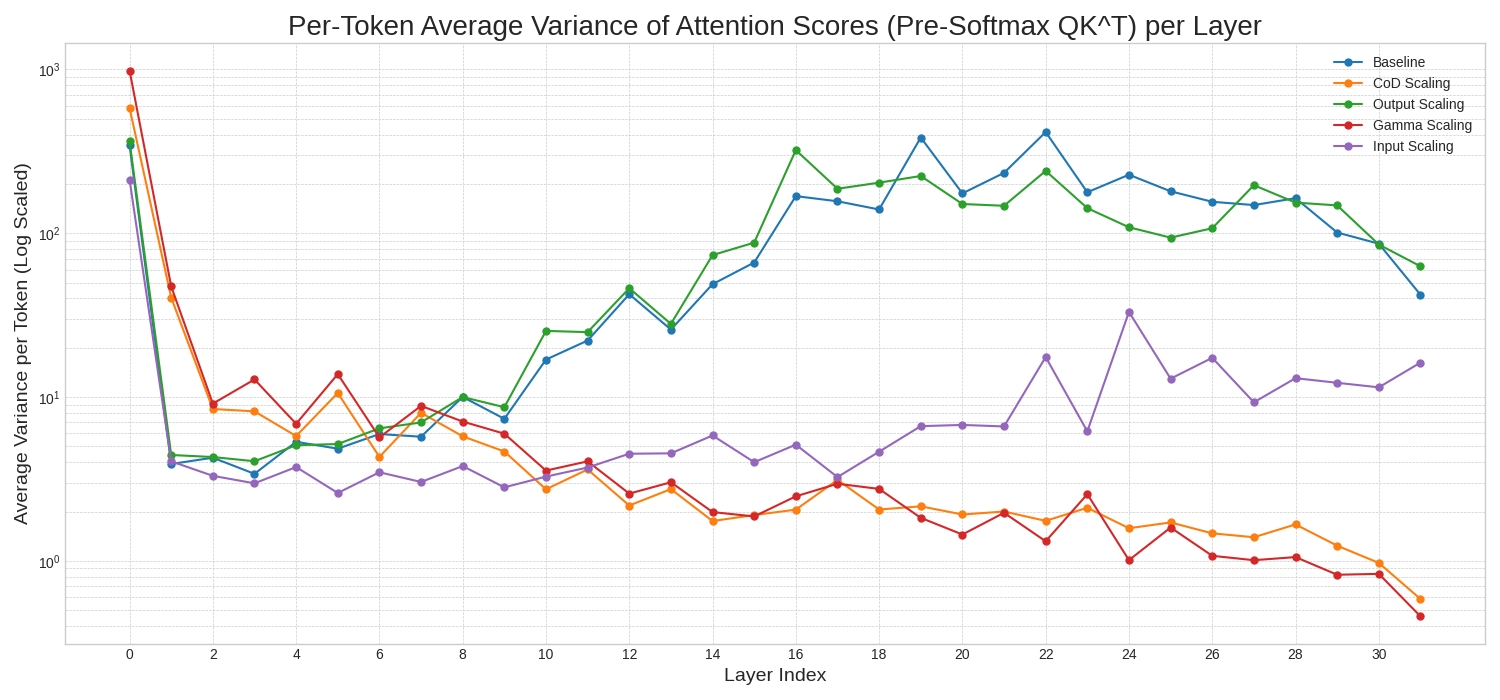
Figure 2 - Average variance of attention scores before applying softmax across the five distinct techniques. The average variance per token log-scaled (y-axis) and the layer index (x-axis).
However, this is an indirect solution - it applies a fix outside the attention block to mitigate a problem inside attention itself. Suppose the root cause of instability is the explosion of attention scores from the QK dot product? In that case, the most direct and effective solution should be to normalize the query and key vectors themselves (Dehghani et al., 2023).
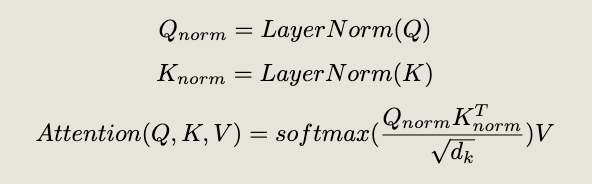
Applying the QK normalization in the Attention Block
Attention is a formula, and if we know that the term inside the softmax is what becomes unstable in later layers, then we can apply a more direct fix by normalizing the queries and keys before the matrix multiplication.
So, with this idea in mind we decided to add the following experiments to our earlier three:
- Baseline + qkNorm: Standard Llama3 2B model, augmented with QK normalization
- Output Scaling + qkNorm: Output scaling model with QK normalization
- Input Scaling + qkNorm: Input scaling model with QK normalization
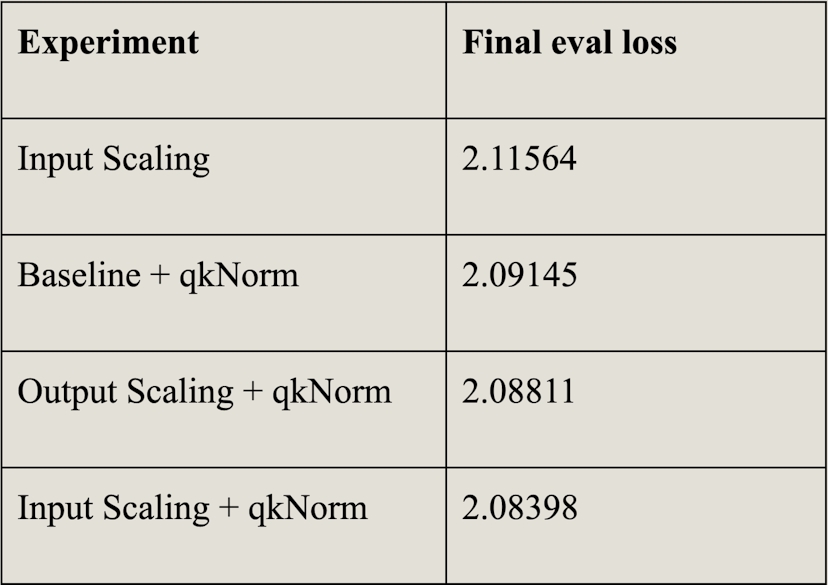
After training over the same configurations as our previous scaling techniques, all three models achieved diminished loss, indicating previous LayerNorm scaling to be a poor man’s QK normalization. By rethinking approaches to scaling, our research has proven to curtail the extent of loss.
The final loss values for these three models are all very similar. Thus, any difference is effectively erased once we introduce QK normalization.
Conclusion
Ultimately, we put LayerNorm scaling to the test, tracing its competency against the Curse of Depth. As our research demonstrates, our scaling strategies, primarily input scaling, have greater functional success reducing eval loss in outer layers. All of the proposed scaling strategies are, however, just an indirect way to normalize QK scores. Yet, the Curse of Depth still haunts us, hindering scalability. Whilst we do not know the causation of continued variance growth in the upper layers, we do know it is not something that can be fixed by simply paying less attention.