Can Overparameterization with SVD speed up training? 

by: Yi Liu, Tom Costello & Julien Darve

Summary

Singular value decomposition (SVD) as a reparameterization of linear layer weights in neural networks has shown promise in existing theoretical and empirical work. However, these have not seen widespread adoption in modern LLMs. In this blog, we revisit this approach, and introduce a novel IIW decomposition to differentiate the effects of orthogonal columns from the overparameterized matrix multiplication. Chiefly, our work hones in on the problematic effect on LLMs. Using Llama-3, our experiments reveal that while overparameterization can increase efficiency for a given base learning rate, it may also degrade training stability.

Main Contributions

1. Our work distinguishes the contributions of orthogonalization from overparameterization using an SVD of the parameters. We introduce a novel form of IIW parameterization as an ablation.

2. Under decomposed parameterization, we observe faster learning at low base learning rates, consistent with Arora et al.’s theoretical work regarding matrix multiplicative overparameterization (2018). In practice, decomposed parameterization setups suffer from training failure at practical learning rates, thereby explaining the slow uptake of this method.

3. We initialize the decomposed matrix parameters given the original weights , and in subsequent updates, the parameters will drift out of their desired decomposition properties. We can choose to re-project every 128 steps, or we can let the parameters learn freely. What we saw: enforcing the decomposition properties with re-projection updates was more likely to cause divergence in training runs.

Motivation and Background

Linear layers in neural networks perform matrix multiplication with learned weights. Past theoretical and empirical work has explored reparameterizing these weights using Singular Value Decomposition (SVD), to impose useful structure, and take advantage of low-rank patterns. Orthogonal representations, in weights, gradients, and activations have been linked to better training stability and generalization. However, SVD-based weight parameterization is still rarely used in large language models. This gap between potential and actual adoption drives our investigation.

The SVD decomposition W = USV^T combines two potentially beneficial properties that, before now, have not been systematically separated:

Orthogonalization: The orthogonal constraints properties of U and V matrices may stabilize training dynamics and gradient flow.

Overparameterization: even though the factorization preserves the presentational capacity, the product structure USV^T fundamentally alters the loss surface geometry.

Previous research has studied these properties in combination, making it unclear which aspect singularly drives performance. This misrepresents the fundamental mechanisms and prevents optimizing the approach for specific applications.

Zhang et al. (2018), in Stabilizing Gradients for Deep Neural Networks via Efficient SVD,  demonstrated that parameterizing weight matrices as W = USV^T can address vanishing and exploding gradient problems. They enforced orthogonality U and V through a parameterization with Householder reflections, in RNNs.

Arora et al. (2018), in On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization, showed that, even on simple convex problems like linear regression, gradient descent can benefit from a non-convex over-parameterization. Most importantly, they verified that this improvement cannot be obtained through the gradients of any regularizer, which highlights the essential role of the multiplicative structure.

Cao et al. (2020), in DO-Conv: Depthwise Over-parameterized Convolutional Layer, demonstrated empirical improvements from overparameterized conv layers. This is consistent with the theory of overparameterization from Arora et al. (2018).

Motivation Experiment in 2D

To further ground our motivations and provide a basis for our work, we trialled a small-scale experiment. Consisting of a simple 2D linear system (Wx = y) with fixed inputs x and outputs y, we learn a 2×2 matrix W through vanilla gradient descent. We then introduce a novel decomposition, termed IIW. In IIW decomposition, we also split a matrix into U, S, and V like in SVD, but with U=I, S=I, V^T=W, to isolate the effects of overparameterization. Further, we explored learning the singular values S as a matrix or vector, and letting the parameters evolve freely or re-projecting to their parametrization at every step. All models began with the same effective matrix, with varying parametrization. Thus, we compared:

Baseline: Direct 2×2 matrix (4 params)

SvecVD: Full SVD decomposition (10 params)

IvecIW: Our novel decomposition (isolating overparameterization, 10 params)

SmatVD: Full SVD decomposition with matrix S (12 params)

ImatIW: Our novel decomposition with matrix S (12 params)

In our 2D experiments, we saw preliminary evidence that overparameterization and re-projection with IIW and with SVD have the potential for faster convergence, as shown in Figure 1. Decomposed methods with re-projection learned fastest, ordered as: IIW with re-projection > SVD with re-projection > IIW without re-projection > SVD without re-projection. Furthermore, matrix singular values converged slightly faster than their vector counterparts. In regards to speed, the square matrix baseline trailed far behind.

Perhaps surprisingly, our overparametrized models, with the exception of ImatIW, curved significantly in their predictions per step, exploring a more diverse region of the parameter space. SVD and training without re-projection caused the most curvature on average. The baseline and ImatIW always remained straight. Overall, our experiment supports both the overparameterization hypothesis and illustrates the potential benefits of maintaining decomposition properties during training.

Figure 1. Convergence visualization of small scale experiments. 

Top row: SVD, IIW, and square matrix (baseline) predictions at each step on a sample run for vector singular value models (left) and matrix singular value models (right). We tested the effects of re-projecting every step vs letting the parameters evolve freely. Overparametrization causes significant deviation from a straight line in model predictions, curving the most for SVD and models without re-projection. 

Bottom row: MSE loss per step averaged over 10 runs per model. We found that IIW and models with re-projection converge the fastest, as well as matrix singular values converging slightly faster than vector singular values. We see convergence plateaus on the scale of 10^-15 for most models, due to the precision limits of float64.

Methods

We originated and fine-tuned experiments using the Llama-3-1B architecture. We used an AdamW optimizer with weight decay 0.01 and context size 1024 on 8 A100 GPUs. Our batch size per gpu was 1, and we accumulated gradients for 8 steps. When running with decomposed parameterizations, throughout the whole network, we replaced all the linear layers inside the attention blocks with this decomposed formulation. See Math Section 1 below for further details of this.

Results

Decomposed parameterizations outperform at low learning rates but destabilize at high rates. At learning rates at and under 0.0002, decomposed methods outperform baseline. At higher learning rates, decomposed methods can diverge while baseline remains stable. See Table 1.

SVD shows no superiority over IIW, suggesting that it is overparameterization, not orthogonality, driving gains. Matrix S parameterization (SMATVD, IMATIW) yields better losses when training succeeds, but instability still persists. Reprojection often increases instability – as evident when we compare the free IIW and free SVD runs to the version that reprojects every 128 steps.

We repeated a similar study on pre-trained weights. The weights are loaded from HuggingFace, but then on initialization they are decomposed into SVD. In this trial, we did not see a large difference between the five parameterizations tested, shown in Table 2.

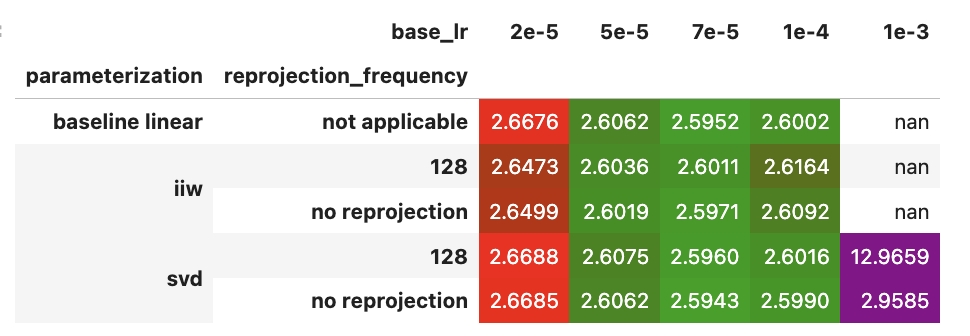
Table 1. Training Llama3-1B from scratch shows that the decomposed parameterization is more robust at very low learning rates but also destabilizes training at higher learning rates. When S learns as a full matrix instead of a diagonal vector, there is a slightly greater decrease in loss when the training succeeds, but the instability remains. Note that the best setting uses baseline linear layers at 0.0005.

Table 2.  Fine-tuning Llama3-1B from pre-trained shows that neither orthogonalization nor decomposed parameterization made a large difference.

Discussion: Theoretical Consistency and Empirical Surprises

Our results align remarkably well with the theoretical predictions of Arora et al. (2018), who proved that overparameterization can provide implicit acceleration in gradient descent. Their key insight was that multiplicative overparameterization acts as a pre-conditioner, accelerating convergence even on simple convex problems like linear regression with Lp loss for p > 2. They provided a framing in which this acceleration cannot be replicated by any simple regularizer – due to its fundamental role in the multiplicative structure.

Our experiments corroborate this theory: that overparameterized decompositions (SVD, IIW, SMATVD, IMATIW) consistently accelerate learning at low learning rates compared to direct parameterization. The fact that IIW performs similarly to SVD strongly supports our theory that overparameterization, not orthogonality, drives this acceleration.

Arora et al.(2018)'s analysis focused on convergence guarantees without addressing training stability. Our empirical results show a limitation: the multiplicative structure also destabilizes training at practical learning rates. This could explain why SVD parameterization of parameters, despite theoretical promise, sees limited adoption in modern LLM training.

Questioning the Role of Orthogonality

The similarity in the performance of IIW and SVD suggests that previous improvements attributed to SVD parameterization may not have actually stemmed from orthogonal properties. Zhang et al. (2018) demonstrated SVD benefits in RNN training, but our results conversely suggest these gains arise primarily from multiplicative overparameterization rather than orthogonal constraints.

This reframing has important implications: overparameterization might be the key mechanism, and it needs to be controlled when studying the orthogonalization of parameters.

In our experiments, enforcing decomposition properties through periodic reprojection often increased instability rather than improving it. One reason behind this could be due to optimizer stats falling stale. This gives weight to the fact that, t especially with overparameterization, the specific properties of the decomposition did not play a major role in our particular setup.

Implications

Our results both explain and highlight the adoption gap of overparameterized decompositions in LLM training. The acceleration effects from Arora et al. (2018) are empirically tangible - we observed consistent improvements at low learning rates. However, the multiplicative structure that enables acceleration may also introduce instability at practical learning rates. Future work should aim to develop frameworks to balance acceleration benefits with training stability.

References

SVD Parameterization: Relevant for discussing ways to parallelize householder matrix multiplication, and make full representations of orthonormal matrices possible.

Zhang et al. (2018): Stabilizing Gradients for Deep Neural Networks via Efficient SVD Parameterization. https://arxiv.org/abs/1803.09327

Mathiasen et al. (2020): Faster Orthogonal Parameterization with Householder Matrices. https://openreview.net/pdf?id=vauMuB-yFkwb

Over-parameterization: Empirical results for overparameterization. Note that they did not show a baseline hyperparameter search.

Arora et al. (2018): On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization. https://arxiv.org/abs/1802.06509 

Cao et al. (2020): DO-Conv: Depthwise Over-parameterized Convolutional Layer. https://arxiv.org/abs/2006.12030